Luftwiderstand
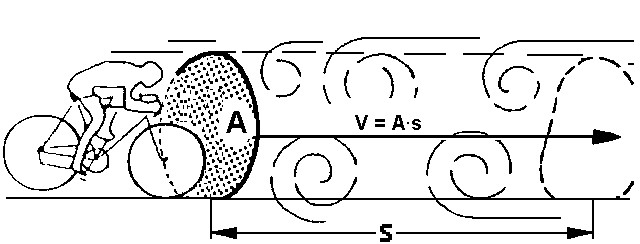
Der Radfahrer in der Abbildung muss eine Kraft aufbringen, um die vor ihm liegende Luft um eine Strecke s wegzuschieben. Diese Kraft ist genau so groß wie die Luftwiderstandskraft FL. Dabei verrichtet der Radfahrer an der Luft Beschleunigungsarbeit. Arbeit ist definiert als Kraft mal Weg: W = F * s. Der Betrag dieser Beschleunigungsarbeit ist also
Durch die Beschleunigungsarbeit erhält die Luft Bewegungsenergie (kinetische Energie)
Kinetische Energie ist definiert durch
Die Masse der Luft errechnet sich aus dem Produkt von Volumen und Dichte (ρLuft). Das Volumen erhält man aus dem Produkt von Querschnittsfläche A und dem Weg s.
Für die kinetische Energie der Luft kann man also schreiben:
Wenn wir mit dem Rad fahren, können wir am Tacho zwar unsere Geschwindigkeit v ablesen, nicht aber die Geschwindigkeit der verdrängten Luft vLuft. Zwar sind beide Geschwindigkeiten bei einer Kreisscheibe oder Reckteckscheibe, welche die Luft wegschiebt, gleich. Je nach der Form des Körpers unterscheidet sich aber vLuft von v. Beide Geschwindigkeiten sind proportional zueinander vLuft ~ v, aber im allgemeinen nicht gleich. Je windschlüpfriger ein Körper, desto geringer ist vLuft im Vergleich zur Fahrgeschwindigkeit. Durch Einführung eines Proportionalitätsfaktors kann man aber aus einer Proportion eine lineare Gleichung machen. Diesen Proportionalitätsfaktor nennt man hier Luftwiderstandsbeiwert und gibt ihm das Zeichen cw. Man setzt also vLuft2 = cw * v2. Wir können jetzt die Geschwindigkeit der Luft durch unsere eigene Geschwindigkeit ersetzen.
Aus den ersten beiden Gleichungen folgt dann:
Die Strecke s kürzt sich weg:
Der Luftwiderstandsbeiwert ist ein empirischer Wert, er wird durch Messungen im Windkanal bestimmt. Die angegebenen cw-Werte gelten nur für eine frontale Anströmung, z.B. beim Fahren in völliger Windstille. Kommt der Wind von der Seite, ändert sich der cw-Wert: Meist nimmt er zu. Für einen Rennradfahrer mit Bremsgriffhaltung setzt man cw gleich 0,88, für ein Tourenrad gleich 1,0. Für ein Liegerad nimmt man einen cw-Wert von 0,77.

Leistung ist definiert durch Kraft mal Geschwindigkeit:
Ein Radfahrer in Rennhaltung fährt mit einer Geschwindigkeit von v = 36 km/h (v = 10 m/s) bei einer Luftdichte von 1,25 kg/m3. Es herrscht kein zusätzlicher Gegenwind. Wie groß ist die Luftwiderstandskraft und welche Leistung muss er gegen den Luftwiderstand aufbringen?
Nun kommt ein zusätzlicher Gegenwind genau von vorne auf mit v = 18 km/h. Die Geschwindigkeit der Luft steigt also auf 54 km/h. Wie groß sind nun Windwiderstandskraft und Windwiderstandsleistung?
Der Gegenwind hat also beide Werte mehr als verdoppelt.
Der Radfahrer reduziert nun seine Geschwindigkeit so stark, dass die Luftgeschwindigkeit wieder den alten Wert von v = 36 km/h erreicht. Er fährt also nur mit v = 18 km/h. Wie wirkt sich das auf Luftwiderstandskraft und Luftwiderstandsleistung aus?
Die Luftwidwerstandskraft ist gleich geblieben, weil sich die Geschwindigkeit der entgegen strömenden Luft nicht verändert hat. Wegen der halbierten Geschwindigkeit ist aber die Luftwiderstandsleistung auf die Hälfte gesunken.
Unser Radfahrer soll 198 W leisten können. Alle anderen Widerstände sollen ignoriert werden. Wie stark muss er seine Geschwindigkeit (v = 36 km/h bei fehlendem Gegenwind) reduzieren, wenn ein Gegenwind von v = 18 km/h aufkommt?
Diese kubische Gleichung läßt sich mit Online-Rechnern leicht lösen. Die richtige Lösung lautet v = 6,974 m/s. Das entspricht 25,1 km/h. Ein Gegenwind von 18 km/h führt also zu einer Geschwindigkeitssenkung von rund 11 km/h, wenn die Leistung beibehalten werden soll.
Bei höheren Geschwindigkeiten spielt der Luftwiderstand die entscheidende Rolle, weil die Luftgeschwindigkeit zum Quadrat in die Berechnung der Windwiderstandskraft einfließt. Ab etwa 15 km/h übertrifft er den Rollwiderstand.
Kommt ein Gegenwind hinzu, kommt man schnell an die Leistungsgrenze und muss die Geschwindigkeit reduzieren. Dadurch verringert sich zum einen die Luftwiderstandskraft quadratisch. Zum anderen sinkt auch die Windwiderstandsleistung, weil hier zusätzlich die Fahrgeschwindigkeit als Faktor eingeht.

